Deep Learning methods have shown that they can be efficiently used to estimate radar parameters on synthetic datasets that were used both for training and performance evaluation1 2. However, applying these methods to real measurement data remains challenging. This is mostly due to the scarcity of labeled measurement data and the associated difficulty of obtaining sufficiently labeled datasets3.
For first and second-order optimization methods, one usually is in need of two things. A step direction and a suitable stepsize to allow rapid convergence. Usually one employs a condition in the form of 1 or uses a so-called Trust-region2 to limit the stepsize during the iteration. If we look at it from another standpoint, we can consider for example a set of various different step directions and we want to find a suitable weighting of those in order to minimize the cost-function as rapidly as possible. Finding these weighting factors is the job of a step direction selection method.
When making use of the Compressed Sensing (CS) paradigm, one has to design the measurement process by means of a suitable compression step. Traditionally, the compression is modelled by means of a linear mapping acting on discretized version of the encountered signals, i.e. a usually complex-valued matrix 1 2 3. Also, it has been an active field of research to apply CS as a data reduction scheme in radio channel sounding 4. Afterwards one is confronted with the problem to recover the parameters of interest, like time-of-flight, direction-of-arrival or Doppler-shifts from spectral-, spatial- and temporal measurements of a radio channel. In this context the iterative maximum-likelihood approach in 4 presents an optimization approach that is both computationally feasible and reproduces closely what is dictated by the Cramer-Rao-Lower-Bound (CRLB).
It has been observed in 1 and Chapter 2.5 of 2 that in channel estimation and modelling a substantial proportion of the transmit energy is not resolveable by a superposition of specular paths, which mostly adhere to a ray of propagation model. These so called diffuse multipath components (DMC) which do not follow the specular ray model pose two challenges.
The ESPARGOS development board1 allows easy access to IQ data obtained from Wifi communications. As such, it efficiently sniffes an environment while providing realtime access to pilot symbols and respective channel state information. This allows to use of parameter estimation techniques based on maximum likelihood like2.
Measuring and characterizing the wireless propagation channel is of utmost importance for developing applications at most recent and unexplored frequency bands. However, since there are no off-the-shelf hardware solutions and no proven algorithms for new frequency bands, doing channel measurements itself is experimental, and the concepts of different research institutions and labs will widely differ. To still develop one common understanding of the wireless propagation channel, concepts for verifying and quantifying the accuracy of the channel sounding results are required1.
Jonas Gedschold; Diego Dupleich; Sebastian Semper; Michael Döbereiner; Alexander Ebert; Giovanni Del Galdo
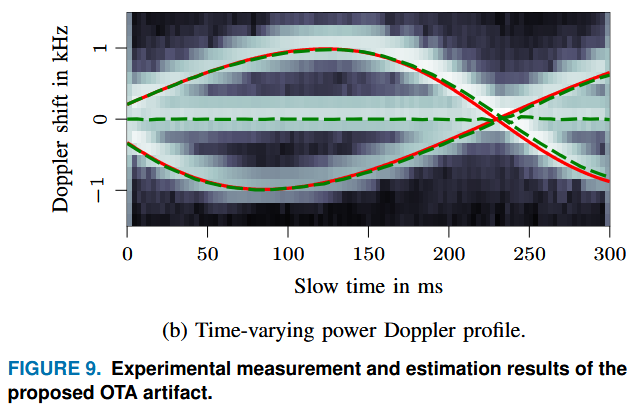
Developing channel models typically requires aggregating channel measurements and the corresponding extracted propagation parameters from different research institutions to form a sufficiently large data basis. However, uncertainties arising from limitations of the sounding hardware and algorithms may greatly impact the comparability between sounding results. Especially, (sub-)THz channel sounders do not allow simultaneous spatially and timely resolved measurements as known from sub-6 GHz and mm-wave applications (right now), limiting the possibilities of a hardware-independent channel characterization. At the same time, a high Doppler bandwidth may occur due to the high carrier frequencies, limiting the time spans for coherent or incoherent data processing. Hence, assessing the sounder’s performance and limits is important before interpreting the measurement results.
